關(guān)于高中數(shù)學(xué)�����,如何計(jì)算點(diǎn)到面的距離公式是最常被問到的問題���,點(diǎn)面距離是指空間中一點(diǎn)到平面中一點(diǎn)的最小長(zhǎng)度。點(diǎn)到平面的距離公式:d=|Ax0+By0+Cz0+D|/√(A2+B2+C2)���。小編也會(huì)為大家?guī)砜臻g中一點(diǎn)到平面的距離公式怎么求的解答�。

一�����、點(diǎn)到平面的距離公式
1個(gè)�����、平面上一點(diǎn)到直線的距離
平面上的點(diǎn) P (x0���,y0)到直線Ax+By+C=0的距離d的公式為:
d=|Ax0+By0+Cz0+D|/√(A2+B2+C2)����。
使用向量法計(jì)算點(diǎn)到平面的距離���,就是把點(diǎn)和平面放在笛卡爾坐標(biāo)系中進(jìn)行計(jì)算�。所以��,點(diǎn)和面都可以用坐標(biāo)表示:

2個(gè)����、空間平面方程
設(shè)平面α在空間中的法向量為(A,乙,C),并通過點(diǎn) P(x0,y0,z0)�����,那么平面方程為:
A(x-x0)+B(y-y0)+C(z-z0)=0
由于該方程使用平面上的一個(gè)點(diǎn)和平面的法向量��,所以稱為平面的點(diǎn)法方程����。
展開上面的等式,然后我們得到平面的一般方程:Ax+By+Cz+D+0����,在,D=Ax0+By0+Cz0����。
二、如何求空間中的空間到平面的距離���?
類似于平面中一點(diǎn)到直線的距離公式����,如果空間中一點(diǎn)到平面的距離為d,空間中點(diǎn)到平面的距離公式為:
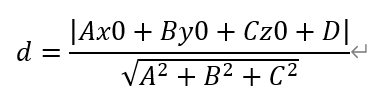

三�����、平面相關(guān)知識(shí)點(diǎn)
為了幫助大家更好的學(xué)習(xí)和掌握點(diǎn)面距離公式的相關(guān)知識(shí)��,小編為大家介紹3個(gè)平面的相關(guān)知識(shí)點(diǎn)�����,包括平面的一般方程�����、矢量的大?��。ㄩL(zhǎng)度)��、向量的點(diǎn)積(內(nèi)積)
平面的一般方程
Ax+By+Cz+D=0
其中 n = (A,乙,C) 是平面的法向量�,D是將平面平移到坐標(biāo)原點(diǎn)所需的距離(所以當(dāng)D=0時(shí),通過原點(diǎn)的平面)
矢量的大?��。ㄩL(zhǎng)度)
給定向量 V(x,他們,z),然后|V|
向量的點(diǎn)積(內(nèi)積)
給定兩個(gè)向量 V1(x1,y1,z1) 和 V2(x2,y2,z2) 那么他們的內(nèi)積是
V1V2 = x1x2 + y1y2 + z1z2

您可以在本文底部的欄中輸入分?jǐn)?shù)以查看您可以上的大學(xué),輸入年級(jí)���、區(qū)域����、選修科目�,一鍵訪問網(wǎng)站,查看更多大學(xué)申請(qǐng)行���、專業(yè)分?jǐn)?shù)和排名����、大學(xué)排名等數(shù)據(jù)��。
同時(shí)�����,還可以通過大數(shù)據(jù)分析和云計(jì)算對(duì)網(wǎng)站進(jìn)行處理���,科學(xué)評(píng)估所有可用的大學(xué)和被我們錄取的概率�����,方便我們填寫以下志愿報(bào)告���,選擇學(xué)校參考����!